Is bad geometry killing free energy?
Researcher Mark Wollum claims that the conventional value of pi is off by one-tenth of one percent. That doesn’t sound like much. But if Wollum is right, it could turn out to be a very expensive mistake.
[Read Mark’s original article from last February, “The Great Pi Conspiracy”]
He says that even such a seemingly negligible error could wreck rotational energy models. And as former Jane’s Defense Editor Nick Cook reports in The Hunt for Zero Point, rotational energy is a key factor in the antigravity and free energy systems that were under development in Germany during World War II and later seized by US forces…then buried under layers of classification and hidden from the world.
Conspiracy researchers have often claimed that secret societies are concealing esoteric information relating to the Golden Ratio (the number phi, 1.61803398875). Dan Brown’s The Da Vinci Code played with that idea.
So what if the big secret is that the true value of pi is based on the golden ratio, as Wollum asserts? And what if that secret information is necessary for advanced work in free energy, antigravity, space exploration, maybe even time travel?
Preposterous? Maybe. Take a look at the final proof offered in this article and see if you can show why it’s wrong.
The Great Pi Conspiracy II: Important Proof Update, Answering Critics; by Mark and Scott Wollum
Our first article detailed this author’s quest for the true number pi, after learning of online claims from multiple sources (Jain, Stefanides, the now defunct vortexspace.org, facebook/therealnumberpi) that we have been using the wrong number for the mathematical constant pi. We offered empirical evidence (by describing our technique for measuring the circumference and diameter of a circular disk to calculate pi) and multiple mathematical approaches to attempt to prove that the true number pi does indeed vary from the accepted textbook value by approximately 1/10th percent. The value obtained empirically from this author varied from 3.143 to 3.145, careful measurements at 3.144, and supported claims that the true value of pi (for linear/circumference functions) is four divided by the square root of the mathematical constant known as the ‘golden ratio’, or more precisely, 3.144605511029693144…, and not 3.141592654 as taught by academia.
In this article we will:
1) provide a brief review of the issue, and talk about the implications of a conspiracy;
2) answer some of the criticism received thus far;
3) This author will critique our (his) former work, and most importantly, withdraw The Previous Final Proof offered in our last article due to serious deficiencies found by this author.
4) In its place we will provide the Revised Final Proof, which thus far appears to this author to satisfy the necessary elements of a more formal proof.
This revised proof uses only basic algebra and trigonometry, and uses the definition of pi to arrive at a unique solution. It should be easier to understand and accept compared to our previous offerings.
5) We provide some references to others who have been pursuing this subject long before coming into this author’s awareness, particularly Mr. Jain and Mr. Stefanides, (sorry for mis-spelling your name last time around- comments were closed before I could respond) and those at The Real Number Pi from facebook, and the apparently now defunct website vortexspace.org. This list isn’t meant to exclude anyone, but contains some of which this author is aware. We don’t know whether our specific approaches have been duplicated; the important thing is to get the word out. I think you’ll find these prior works (Jain, Stefanides) quite detailed, insightful, and fascinating.
One of the main reasons for even putting my name to the first article was to pay tribute to my late brother Scott, who was a true math genius and had a way of re-defining issues which enabled simple solutions to seemingly complex problems. So I again pay tribute to my brother Scott and all those seeking the truth who have the insight to recognize belief systems and challenge their own assumptions when confronted with conflicting evidence. And we challenge those in academia to have the courage and show enough intelligence to challenge their own belief systems in pursuit of knowledge, in spite of severe political pressure to maintain the status quo.
And we thank Dr. Barrett for the courage to publish this, in spite of his continual doubts about the validity of this proposed new pi. Dr. Barrett’s love of truth, had cost him his job and livelihood when he was politically hounded out of academia for his personal political views (which had little to do with his actual course curriculum addressing Arab Studies). And he continues to challenge his silently-complicit peers to explain how steel-framed high rises can collapse at or near free-fall acceleration without controlled demolition. As of this date, not one of his peers have accepted a $2000 stipend to confront him in a 90-minute debate to tell him why he is wrong.
Brief Review- Why is Pi Important?
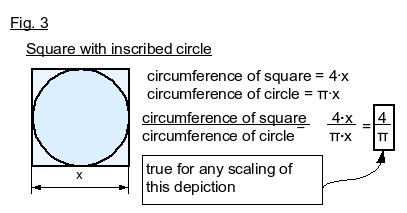
Pi the mathematical constant defines the ratio of the circumference of a circle divided by its diameter. Comparing this curved distance to its linear counterpart, it also defines the relationship between a circle and the square which circumscribes (surrounds) it, in which the circle and square intersect at only four points. The ratio of the circumference of any square divided by the circumference of it’s inscribed circle, is, by definition, 4/pi. We will see that this definition lends itself to an algebraic derivation of the true number pi.
Pi is arguably one of the most important physical constants in the universe.
Its value defines the relationship between matter and energy in our rotational models- everything from the cosmos to sub-atomic particles, because pi is used in energy calculations in anything with rotational energy. If pi isn’t correct, the mass/energy ratio isn’t correct.
The Pi Conspiracy
We propose that there are entities who know the true number pi, but for whatever reason, keep it’s value hidden. Are there secret societies which know this, and maintain this secrecy as a form of intellectual supremacy? We do not know, but we can assume that there are formal agencies which have to know the true number pi, but choose not to divulge this information. NASA for example, has to know the true number pi in order to accurately predict the behaviors of their satellites. So it would be a fair assumption that some level of conspiracy must exist to keep this knowledge hidden. Perhaps key personnel have gag orders or non-disclosure agreements. Perhaps the true number pi is stealthily programmed into their modeling software. Who knows?
Think about this for a moment. I am proposing a massive global conspiracy to keep hidden certain knowledge. Many people, perhaps even most, will defend the orthodox position out of good faith, simply believing in the infinite-sided polygon nonsense even in the absence of any proof or any supporting evidence whatsoever, apart from the fact that the textbook pi approximates the circumference of a circular disk to within three (and only three) significant digits.
I have been given suggestions that I should talk to professors at universities, or perhaps contact the people at CERN and ask for disclosure of the dimensions of their massive round collider. Again, think about this! Would anyone make these suggestions if they understood my accusations or believed there was any possibility that myself, Mr. Jain, Mr. Stefanides, or anyone else might actually be right? If this were true, wouldn’t there be someone, somewhere, at some university who understands that the very foundation of our math and physics models is built upon logical contradictions? Who could you trust for honest disclosure? That makes as much sense as asking the Pentagon- ‘Who was responsible for 9-11’?!
I’ve been through the university system as an undergraduate, (not to be confused with our state’s higher technical/vocational education system, which I found to be excellent), and can attest to the notion that the university’s main function is indoctrination into particular belief systems. If one has a good memory, one can be very successful academically by simply regurgitating all the answers that they want to hear. (My poor short-term memory made college difficult). There need be very little thinking or problem-solving ability. Indoctrination into various professions values quantity over quality. Sure, the engineers have to be able to solve some problems- those problems as defined by the establishment. But improper framing of problems already sets one up for failure, and can perpetuate dysfunction systems. The solutions are designed to benefit corporations and existing power structures, not necessarily humanity. Hence the push to receive corporate funding for state universities. Increased corporate funding of public education will surely destroy what is left of our academic institutions, as surely as corporate funding has greatly diminished the ability of our public media to serve the public interest.
Answering the Critics
Here are a few responses to some of the criticism/comments offered.
The limit of the infinite-sided polygon approach that we presently use to calculate the circumference of a circle just seems intuitive.
A true circle, as originally defined, is a collection of points on a given plane which are all equidistant from a single point on said plane. This is the definition I was taught several decades ago. As far as I know, no one has ever offered proof that the limits of an infinite-sided polygon (apparently the newer definition of a circle) are the same as a true circle. If there were such a proof, the mathematicians wouldn’t have had to change the definition of a circle to equal the limits of an infinite-sided polygon. That whole process itself is a logical contradiction, and this author claims it is, or should be, mathematically undefined.
Infinity doesn’t exist in reality because, by definition we can never attain it. But infinity exists as a limit because we can approach it. There are two infinities- positive and negative, that is, infinitely large and infinitely small. The perimeter of an equal-sided polygon equals the number of sides times the length of each side. With an infinite-sided polygon, we have an infinite number of sides whose lengths are infinitely small. The process of multiplying positive infinity by negative infinity is self-contradictory and undefined. How can this process have a physical correlate? How can an entity which is undefined even exist as a conceptual limit? It can’t. That makes as much sense as having a crooked straight line or a round square.
If the concept of infinity is difficult to grasp (it is for me), let’s put it aside and simply consider a polygon with a very large number of equal sides. These can exist. It doesn’t matter how large- 10 thousand, 10 million, 10 billion, or 10 trillion times 10 trillion. The perimeter of any polygon, no matter how many sides it has, will ALWAYS be smaller than the perimeter of its circumscribed circle. And the perimeter of such a polygon, as you increase the number of sides, will never approach the perimeter of its circumscribed circle because THEY ARE TWO DIFFERENT MATHEMATICAL ENTITIES! Our Proofs demonstrate this. The same thing can be said for a circle with a circumscribed polygon. The circumscribed polygon will always have a circumference which is greater than its inscribed circle, no matter how many sides it has. And we are contending that it makes no sense to talk about the limits of an infinite-sided polygon because such an entity is, or should be, undefined.
I don’t know at what point the definition of a circle was changed, or what was the rational for doing so. Was the definition always the limits of an infinite-sided polygon, and I was transported to an alternate reality? I doubt it. Some reading this may be old enough to know the answer. Maybe the mathematicians needed a quick fix for contradictions posed by their illogical definition, or needed a way to help perpetuate deception, or maybe a legal way to avoid being charged with fraud. Who knows? But I will re-state emphatically- A true circle is a collection of points on a given plane which are equidistant from a given point on that plane! That is not the same as the limits of an infinite-sided polygon, which is a logical contradiction, undefined, and therefore cannot possibly have a physical correlate!
Several critics have offered these:
Perfect circles don’t exist in reality. Or the reason I can’t use the textbook pi to accurately predict the circumference of a circular disk is because that is the difference between theoretical science and applied science (that last one from someone with a PHD degree, who offered no reasonable explanation why the two pi numbers, the measured VS the theoretical, should be so far apart).
A true circle is a mathematical concept. But the first day in basic geometry class we are taught that these concepts have physical representations. How accurate can these representations be? If we grind a round disk on a spinning lathe, all points along the edge will be the same distance from the center of the disk, as accurately and as smooth as the machining process allows. We can measure the circumference of a disk accurately to four significant digits using equipment which costs $20. And we don’t even need a perfect circular disk. The circumference of a circle equals pi times the diameter. Being a linear function (no exponents), all we have to know is the average diameter. We can take multiple diameter readings, and simply use the average diameter multiplied by pi to accurately predict the circumference of our disk. This is basic math and basic mechanics. This evidence alone was enough to convince this author that there could indeed be a serious problem with the textbook value of pi. And it astounds me that some people with advanced degrees don’t get this.
If a theoretical pi value cannot survive empirical measurement to at least 4 significant digits, it cannot possibly be correct.
A better argument would have been that there must have been undetectable slippage when rolling the disk to obtain it’s circumference, or perhaps I just measured wrong. But those arguments weren’t used. Perhaps people didn’t want to encourage others to actually try measuring the circumference and diameters of a round disk, because of the discrepancies which would be revealed. I encourage others to try this. See first article for more details.
The left Riemann summation of the function of a circle with n = 10, 000 yields a pi number which is already smaller than our proposed new pi. So the new proposed pi cannot be correct.
I found this to be the most interesting and perhaps revealing comment.
The Riemann summation is a method of approximating the area under a mathematical curve by dividing the area up into very small rectangles (‘n’ number of rectangles), and adding those areas up to approximate the area. The left Riemann sum will over-approximate the area. (There are some good online references if one wants to go further into this.)
This line of argument isn’t really relevant to our claims, as we are referring to the pi constant which defines the circumference of a circle to it’s diameter. We said nothing about area calculations. But this may be an important topic.
Using an online reference to calculate the Left Riemann sum, with n = 10,000, does indeed seem to produce a smaller pi value than what we propose, if you take the formula for the area of a circle as pi times radius squared. But think about what we are saying. We are proposing a radical mis-understanding of circle geometry, and need to re-evaluate all of our assumptions about circle geometry in light of conflicting evidence. Unproven assumptions need to be challenged!
Everything needs to be logically consistent. All of our assumptions need to be re-examined.
In this article we are offering a newer math proof (at least new to this author) which seemingly provides a solid basis to discredit the old transcendental pi number for circumference functions. (Following in the heals of other authors)! The new proposed pi also seems to be supported empirically.
We propose there are at least two other logical possibilities which need to be considered regarding the left Riemann summation:
1) Either there is a problem with the algorithms used for calculations of the left Riemann sum, or
2) We need to re-think the derivation of the formula for the area of a circle.
3) Can you think of any other logical possibilities? I presently cannot, unless someone can point out any possible conceptual flaws in the Riemann Sum. (Wouldn’t it be ironic if the dysfunctional transcendental pi was perpetuated by a faulty formula for the area of a circle?)
In the online reference for the Riemann sum, using n = 10,000, they actually listed all 10,000 values, but they were listed in such a way that it was very difficult to correlate the input numbers with their respective output values (making it difficult to be confident in the result). Also, since some of the terms become very small, any calculation of this sum needs to carry enough digits to maintain a given degree of accuracy. The online calculator might have been adequate for this, but we are not sure.
Keep in mind that if the old pi is wrong as we are asserting, then all the preprogrammed functions for pi and trig functions which depend on it, and any algorithms which use these values, in every calculator and software program in the world, are fundamentally flawed!
If you eliminate the impossible, whatever is left has to be probable.
Special note to any of my associates who may dismiss this out of hand before even hearing the full argument. (And to protect the innocent, their name does NOT rhyme with ‘gets her’.)
Dismissing anything out of hand before hearing a full argument, no matter how preposterous it may sound, is a sign of ignorance and inability to challenge potential belief systems.
This story is far from finished, only beginning. We expect these new findings to overturn centuries of flawed concepts, and negate any theorems which are dependent upon the old transcendental pi number. For a $10,000 grant, I would gladly maybe spend another year staring at circles, squares and triangles, to further explore these issues. (Please contact the editor with any offers!). Absent any grant, I can’t afford the time, and there are many others who have much more skill at this than I do. And they will find the answers, if they only know to look for them!
Author’s Critique of His Own Previous Work from the first article, The Great Pi Conspiracy
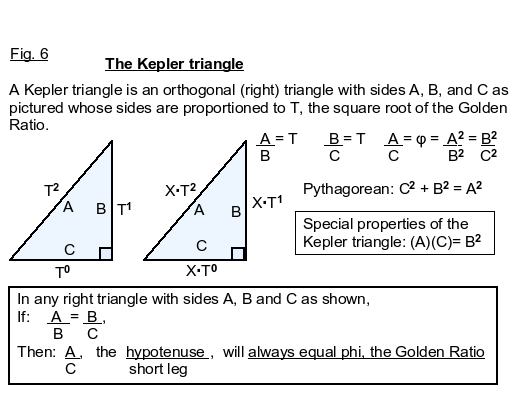
We had offered three of our own different math approaches to try to resolve these issues. I had so many failed attempts during this process, which at first appeared good to me, but later revealed some flaw (always found by this author). Without much exaggeration, this process may have happened 30 or 40 times. It happened so often, I wondered whether pi might be something else entirely, and not related to the Golden Ratio, wondering if those claims were put forth to further conceal the truth. But in all of our explorations, 4/pi and T, the square root of the Golden Ratio were algebraically and geometrically indistinguishable from one another.
In the last article, my first two approaches used somewhat unconventional techniques, which although logical, I didn’t think they would necessarily convince the academics. So the final proof was offered. One of the fundamental criteria for a formal proof is that it must demonstrate one and only one solution, if indeed only one solution exists. On these grounds we are not sure about the first two, but the previous final proof does not appear to pass this test. In haste to be done with this project, it was not adequately reviewed by this author. In that last proof I had identified an exception to my argument, but explained it as having changed the definition of the symbol pi used in the proof. This was not adequately explained. Taking another look at it after publication, I had reservations about its validity. As it turns out, you will see that any value for ‘S’ within a reasonable range will yield the same equation, so we did not demonstrate a unique solution, in the confusing format in which the proof was presented. Comments had been closed by the time I realized a problem. Attempting to clean this up resulted in many more failures, but continual new insights which kept us going. I also didn’t want to disappoint my late brother, in whose joint name I offered these works.
In the process of trying to salvage the previous final proof, I was able to find a different approach in what I believe is more definitive, as it appears to have all the elements required of a formal proof. This one should be much easier to understand.
Here we use the definition of pi using a circle’s relationship to its circumscribed square, derive a value for pi and demonstrate only one solution. We use only basic algebra and trigonometry, with nothing unconventional.
It is surprisingly, if not embarrassingly simple. And I welcome any critique which can point out any logical flaws in it.
Revised (New) Final Proof
Overview:
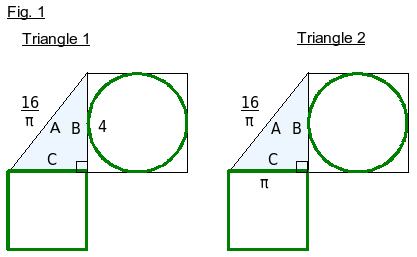
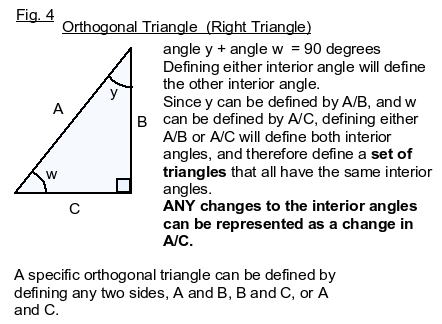
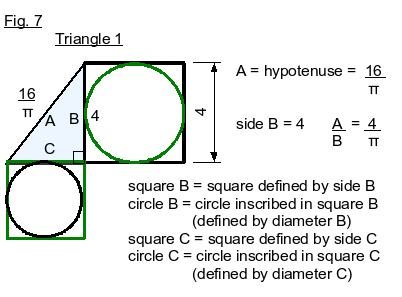
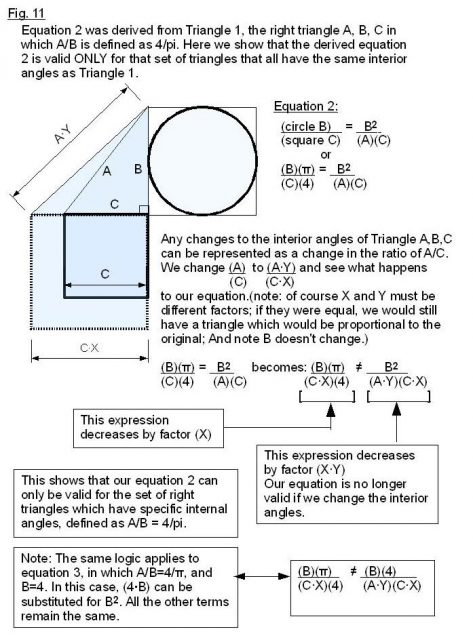
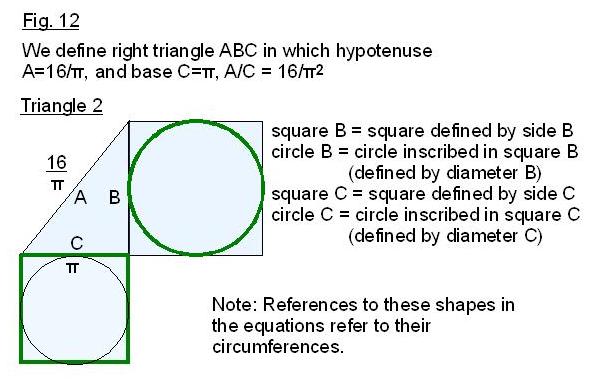
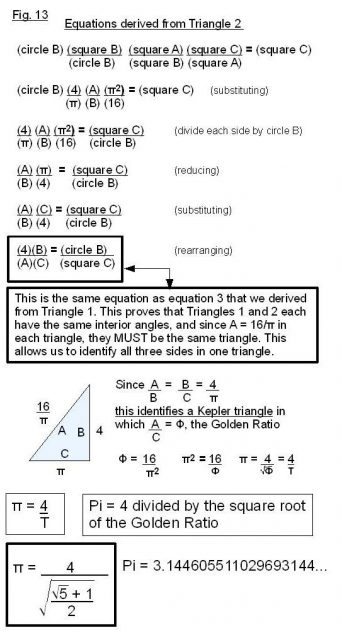
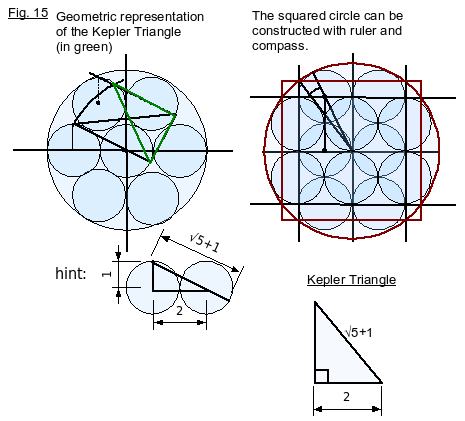
We will prove the new pi by proving that triangles 1 and 2 in Fig. 1 are the same triangle. We do this by deriving an equation for triangle 1, using the definition of pi to describe the relationship between circle B (the circle defined by diameter B) and the square defined by side C. We then show that this equation (equation 2) is valid only for the set of triangles that have the same internal angles as this triangle 1. We refine the equation (equation 3) to describe one specific triangle in that set, in which A, the hypotenuse, equals 16/pi. We then derive the same equation for triangle 2 which defines the relationship between circle B and square C in triangle 2, proving that triangles 1 and 2 have the same internal angles. And since triangles 1 and 2 also have the same length hypotenuse, they must in fact be equal triangles, giving us the lengths of all three sides. This proves that pi is expressed in a Kepler triangle, whose hypotenuse/base must equal the Golden ratio, or 16/pi squared. Hence, pi must equal 4 divided by the square root of the golden ratio.
Brief Proof Outline:
The figures should be fairly self-explanatory.
Figures 1 through 6: definitions needed to understand the proof;
Figures 7 through 13: body of the proof; the derivation of pi.
Figure 15: a geometric interpretation of the squared circle using the new pi;
Definitions:
Derivation of Pi:
This solution for pi is derived from the definition of pi (using a circle’s relationship to its circumscribed square) and defines only one unique solution.
Since the old transcendental pi is inconsistent with this derivation, the old transcendental pi is inconsistent with its own definition and cannot possibly be correct.
Since the old transcendental pi is inconsistent with its own definition, it cannot possibly be correct.
Can you find any flaws here? I haven’t yet.
The new pi based on the square root of the Golden Ratio is the number you will get if you try to calculate pi to four significant digits by measuring the circumference and diameter of a circular disc. This is the pi that is needed for physics equations which define energy in rotational systems.
Note: I have not tried (and am not able) to fix all of the problems with our erroneous concepts regarding circle geometry. I believe this material, along with the work of others (some I have referenced) should provide a reason and framework for others to investigate further, and help alert others to adopt the new pi. I realize this information may spark awareness of other contradictions. But to sort it all out, we must re-examine our current concepts, and question that which is based on unproven assumptions and logical contradictions. It is possible, if not likely, that this new awareness will only come from a bottom-up grassroots movement, as the elite don’t appear willing to even look at this issue.
Special note to Mr. Jain and Mr. Stefanides, feel free to check in, would love to hear from you. If you can provide more links we will try to include them. I encourage everyone to support their work. Your works have been paramount to increasing awareness of this very important topic. Someone from facebook had checked in last time, and stated that this idea for revising our pi value was given to us several decades ago by contact with human beings of extraterrestrial origin. We find this idea fascinating. If any ET humans are around, please get in touch, would love to meet for coffee.
To summarize, I am asking the reader to consider:
1) that our entire concept of circle geometry is built upon logical contradictions and unproven assumptions.
2) that pi, one of the most important physical constants in the universe, is actually,…um…a physical constant.
3) that physical constants have representations in the physical world.
4) that representations of physical constants can be approximated with physical measurements with a given degree of accuracy.
5) that physical measurements of pi, and relatively simple mathematical proofs, are inconsistent with the textbook pi (referenced in these articles as ‘the old transcendental pi’).
6) that the existence of these contradictions necessarily implies a conspiracy to keep this knowledge hidden.
Do you want our ET friends to think we’re all just that bloody stupid?! It’s a conspiracy! That’s my story and I’m stickin’ to it…
In memory of my late brother, Scott, Wollum.

Dr. Kevin Barrett, a Ph.D. Arabist-Islamologist is one of America’s best-known critics of the War on Terror.
He is the host of TRUTH JIHAD RADIO; a hard driving weekly radio show funded by listener donations at Patreon.com and FALSE FLAG WEEKLY NEWS (FFWN); an audio-video show produced by Tony Hall, Allan Reese, and Kevin himself. FFWN is funded through FundRazr.
He also has appeared many times on Fox, CNN, PBS, and other broadcast outlets, and has inspired feature stories and op-eds in the New York Times, the Christian Science Monitor, the Chicago Tribune, and other leading publications.
Dr. Barrett has taught at colleges and universities in San Francisco, Paris, and Wisconsin; where he ran for Congress in 2008. He currently works as a nonprofit organizer, author, and talk radio host.
ATTENTION READERS
We See The World From All Sides and Want YOU To Be Fully InformedIn fact, intentional disinformation is a disgraceful scourge in media today. So to assuage any possible errant incorrect information posted herein, we strongly encourage you to seek corroboration from other non-VT sources before forming an educated opinion.
About VT - Policies & Disclosures - Comment Policy